Understanding Validator Effective Balance

---

Proof of Stake

A key requirement of any blockchain is its ability to secure its chain. A secure chain is one in which transactions are verifiable and immutable i.e. by referring to the blockchain someone can obtain the details of a transaction that took place, and be sure the details are not faked and the transaction cannot be altered retrospectively.

Ethereum 2 allows individuals to help secure the network by running validators. A validator is a computer process that can be thought of as a voter: every time a new block is built on the network a defined subset of the validators consider the block and decide if it contains valid transactions, links itself correctly to the previous block in the chain, etc. If the validator is happy the block is valid it can attest the same. When a block obtains enough attestations by the validators it is considered canonical¹

To encourage validators' good behavior, and to avoid the situation where validators either don't bother to attest to blocks or actively lie about the validity of blocks, their actions have monetary consequences. Before a validator can start to attest it needs to submit a one-off deposit of 32Ξ (Ether) with the network; this forms the validator's initial balance. Every six and a half minutes or so the network measures the actions of each validator and issues rewards or penalties appropriately that accrue to the validator's balance. The amount of the reward or penalty depends on the current balance of the validator; attesting with a higher balance provides larger rewards and penalties than attesting with a lower balance.

It is important to understand the key concept of rewards and penalties: rewards are given for actions that help the network's process to reach consensus, and penalties for actions (or inactions) that hinder it. As such, validators that maximize their rewards also provide the greatest benefit to the network as a whole.

A detailed explanation about Ethereum 2's proof of stake model is beyond the scope of this article, but the important thing to understand is that each validator has its own balance that is updated periodically by the Ethereum network rules as the validator carries out its duties (or not).

This article explores the relationship between a validator's balance and the rewards and penalties it accrues; if a validator is attempting to provide the highest benefit to the network, and hence obtain the highest rewards, there are a number of subtleties that must be properly understood.

---

Rewards and Penalties over Time

As mentioned above, when a validator carries out its duties it is rewarded and when a validator does not carry out its duties it is penalized. Rewards and penalties over time are reflected in the balance of the validator, as shown below for a fictional validator:

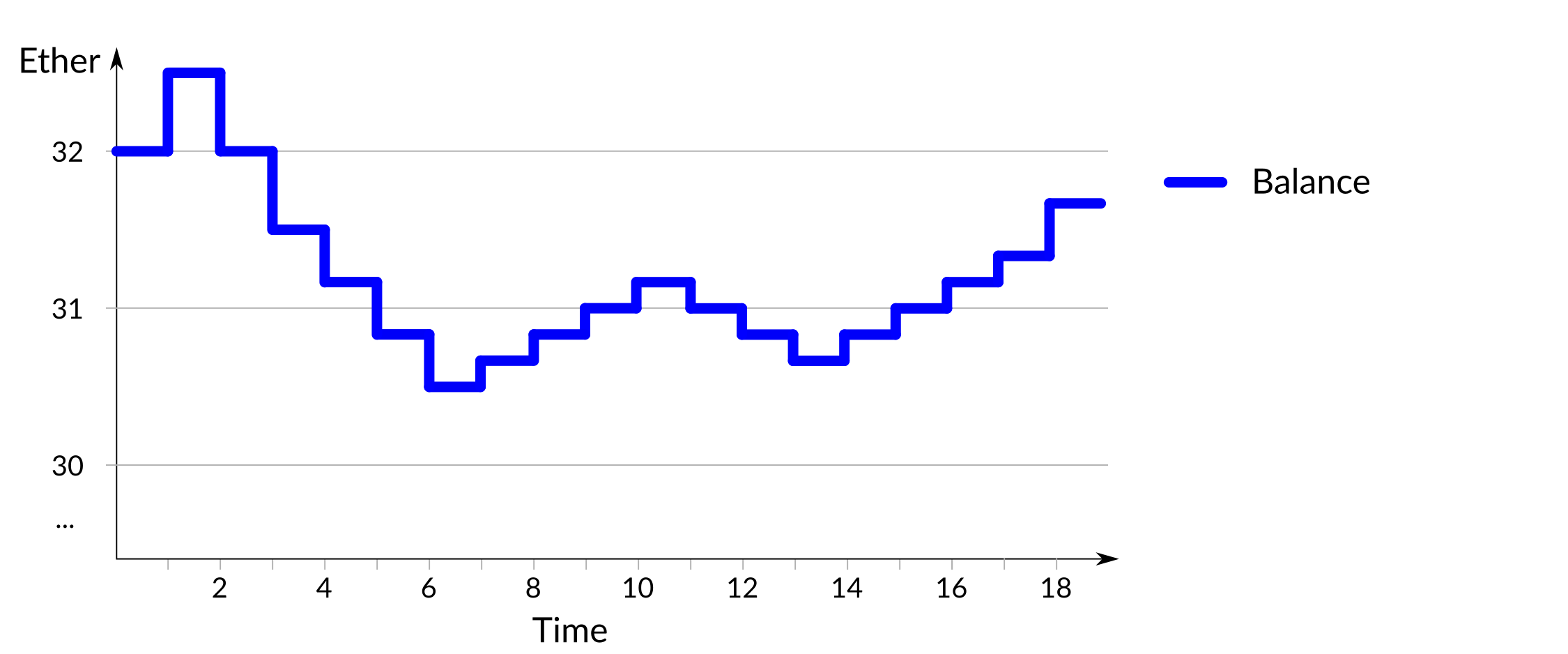Figure 1: A fictional validator's balance over time

(Note that the size of rewards and penalties in this and subsequent graphs have been exaggerated to more clearly display their relative sizes.)

At each time 1, 2, 3, etc. the validator's participation is assessed and it is rewarded or penalized accordingly, resulting in a step change in its balance. This particular validator has periods of participating correctly and being rewarded, and periods of non-participation and being penalized:

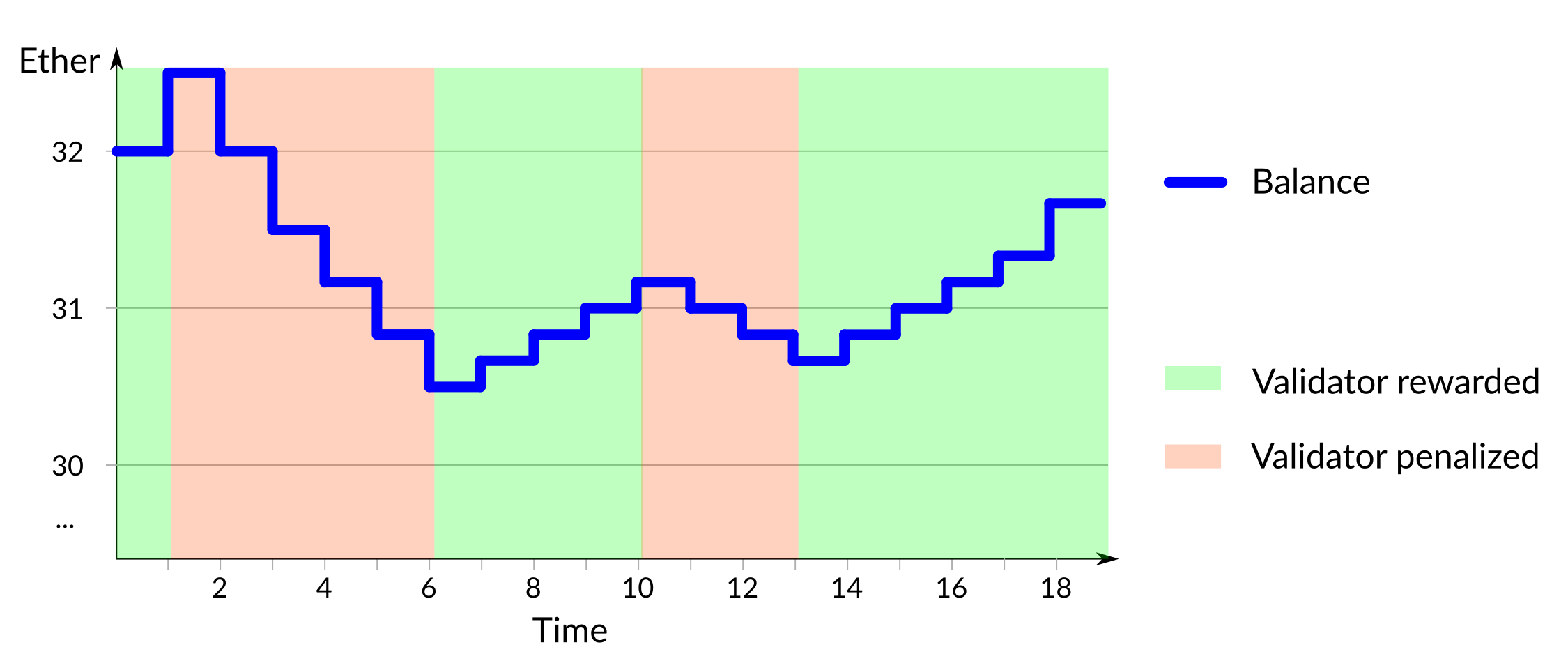Figure 2: Phases of rewards and penalties

The size of the rewards and penalties changes at different times throughout the graph in a non-obvious fashion. For example, the penalty given at time 5 is significantly larger than penalty given at time 13, even though the balances at those times are the same. There are four points of particular interest on this graph that deserve closer consideration.

The first point of interest is at time 3, which is highlighted below:

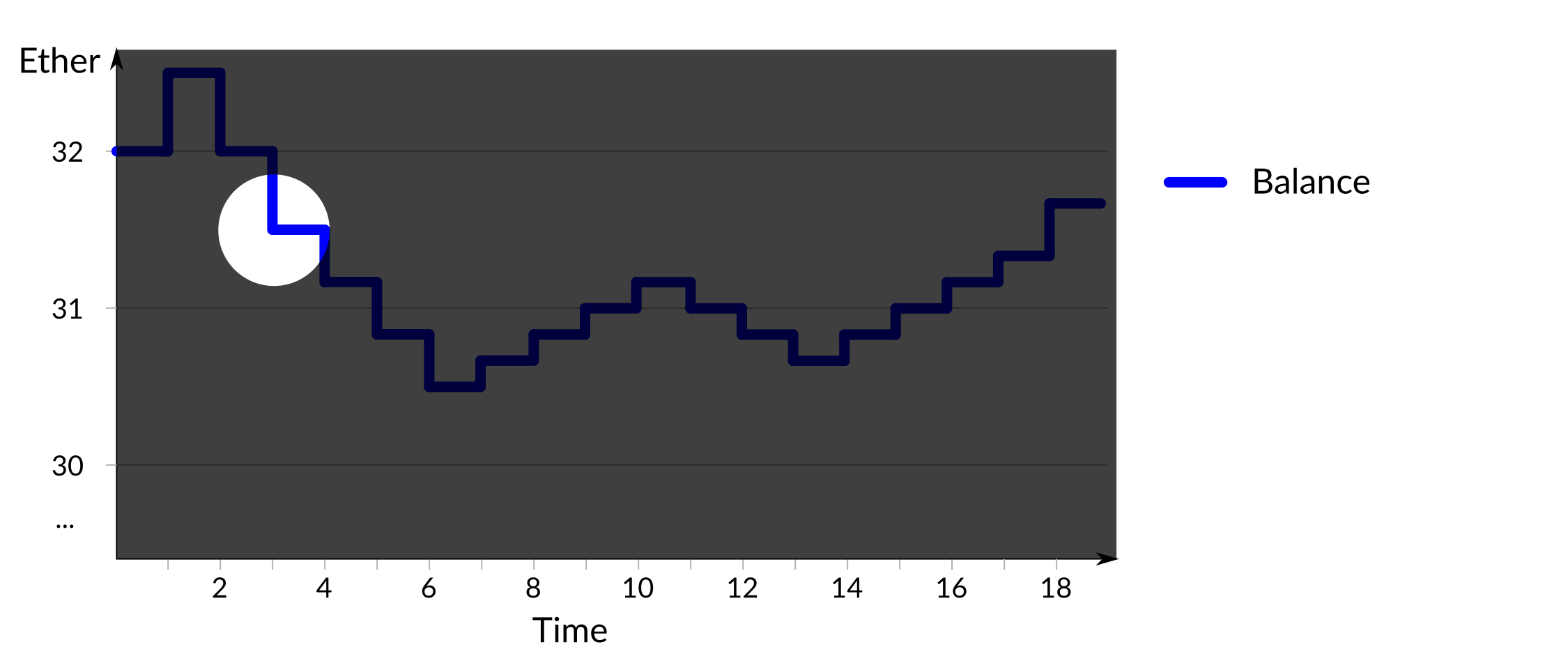Figure 3: Reduction in reward/penalty value

At this time the balance in the validator has dropped below 32Ξ, and the size of subsequent rewards and penalties decreases for no clear reason.

The second point of interest is at time 5, which is highlighted below:

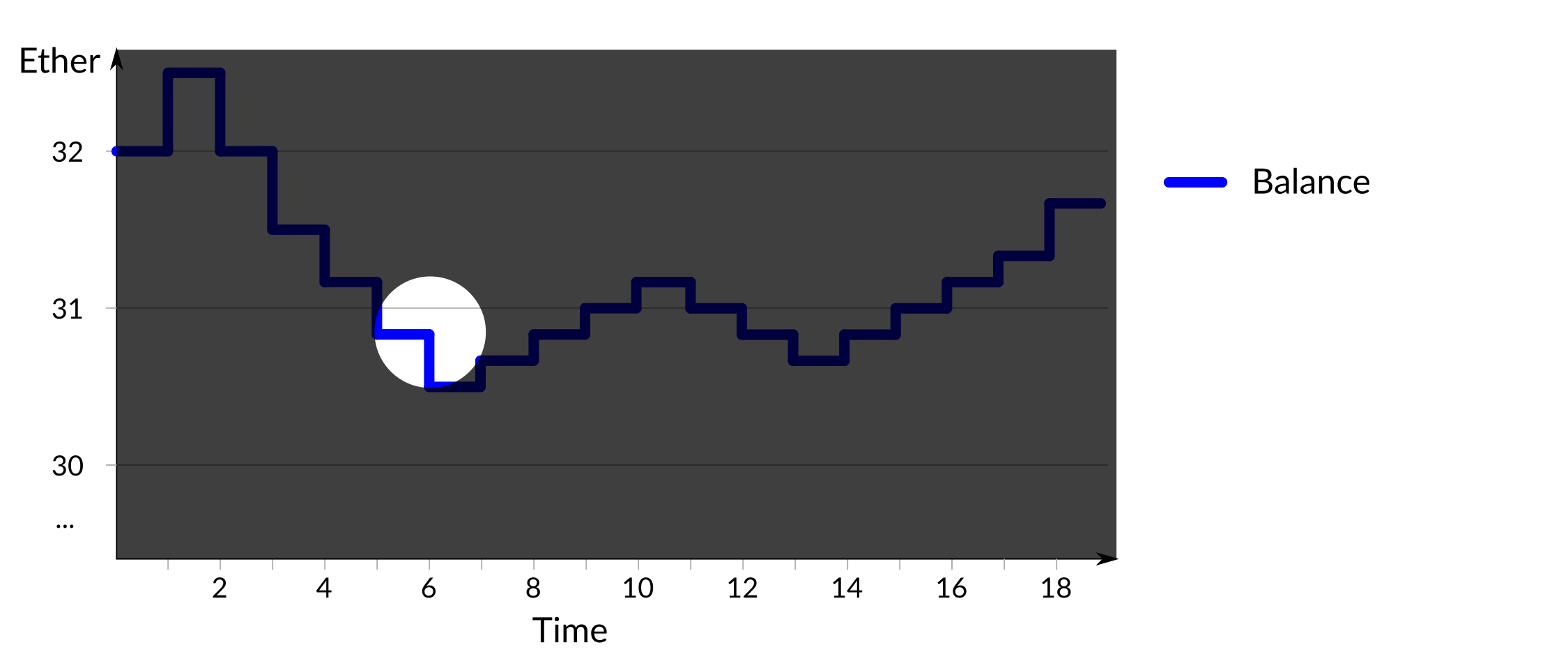Figure 4: Non-reduction in reward/penalty value

At this time the balance in the validator has dropped below 31Ξ, but the subsequent penalty is the same as the previous time, which is inconsistent with the change at time 3.

The third point of interest is at time 9, which is highlighted below:

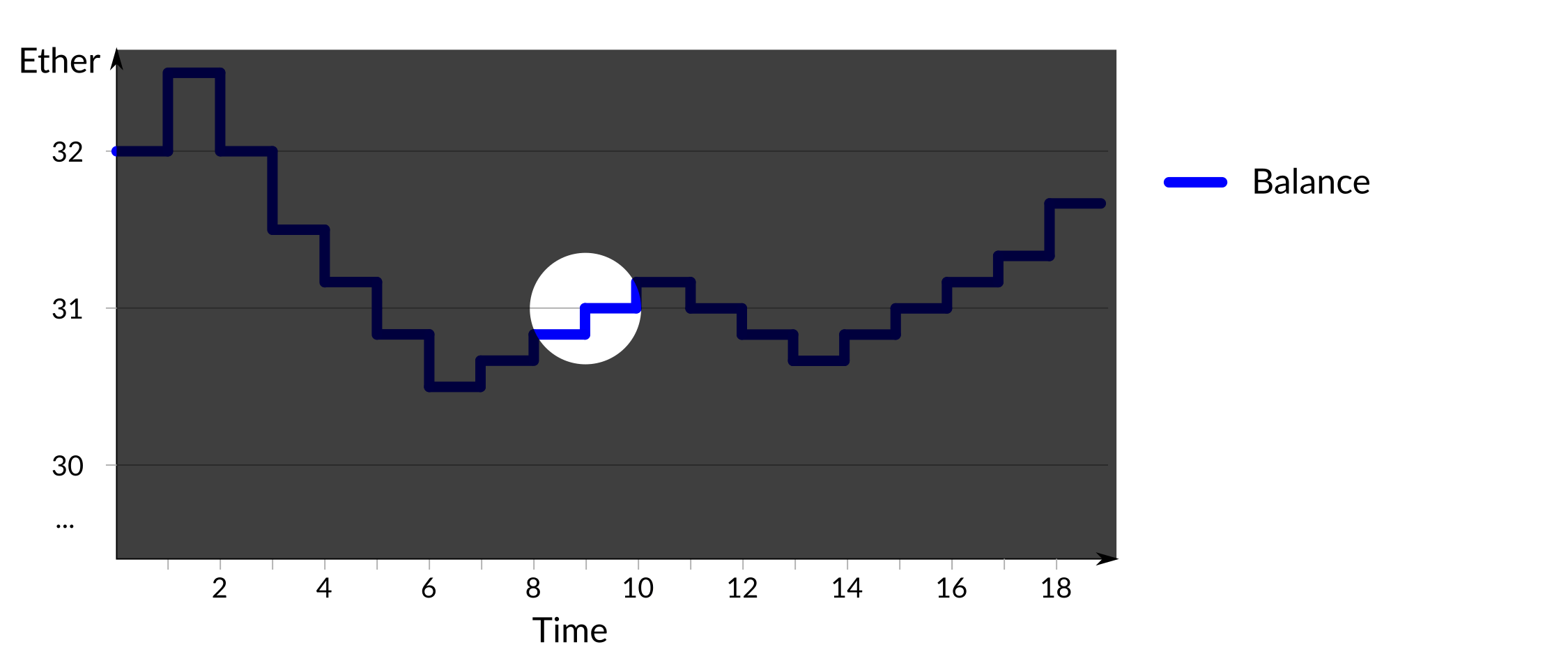Figure 5: Lack of expected increase in reward/penalty value

At this time the balance in the validator has increased back to 31Ξ, however the size of subsequent rewards and penalties remain the same as when the balance was below 31Ξ.

The fourth and final point of interest is at time 18, which is highlighted below:

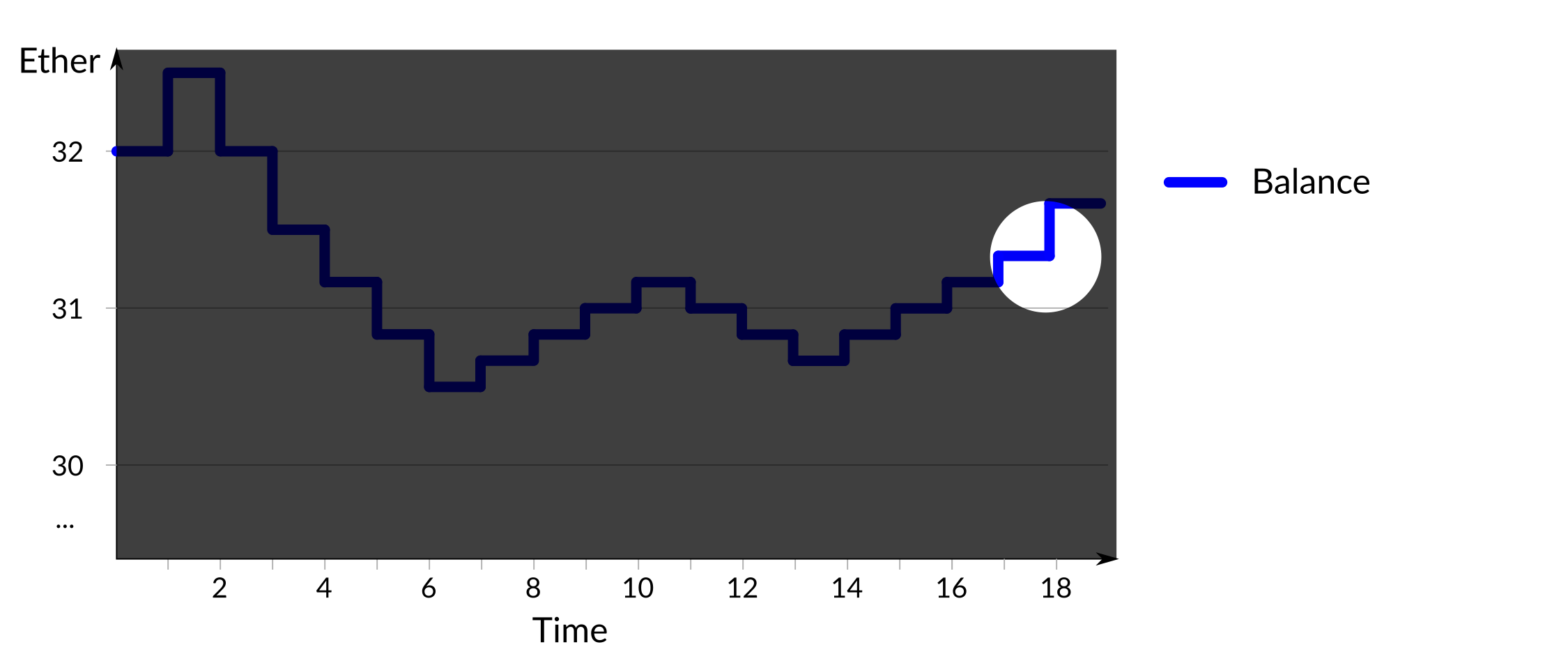Figure 6: Unexpected increase in reward/penalty value

At this time the size of rewards and penalties increases, although the balance has not appeared to pass any significant point.

All in all these paint a chaotic view of the rewards and penalties. To understand why these rewards and penalties are the size they are requires an understanding of effective balance.

---

What Is Effective Balance?

Effective balance is a value for each validator that is derived from the validator's balance and prior effective balance. It is used to calculate the size of rewards and penalties given to that validator.

1. Effective balance can never be more than 32Ξ. This means, for example, that if a validator's balance is 100Ξ its effective balance will be 32Ξ
2. Effective balance is always a multiple of 1Ξ, with any additional balance being ignored. This means, for example, that if a validator's balance is 29.7Ξ its effective balance will be 29Ξ, with the extra 0.7Ξ ignored for reward and penalty calculations
3. Effective balance will only increase if the validator's balance is more than 1.25Ξ higher than its current effective balance. This means, for example, that if a validator's effective balance is 25Ξ its balance must increase to more than 26.25Ξ before its effective balance will increase to 26Ξ
4. Effective balance will only decrease if the validator's balance is more than 0.25Ξ lower than its current effective balance. This means, for example, that if a validator's effective balance is 25Ξ its balance must decrease to less than 24.75Ξ before its effective balance will decrease to 24Ξ

Following the above rules allows the addition of a line showing the validator's effective balance to the chart:

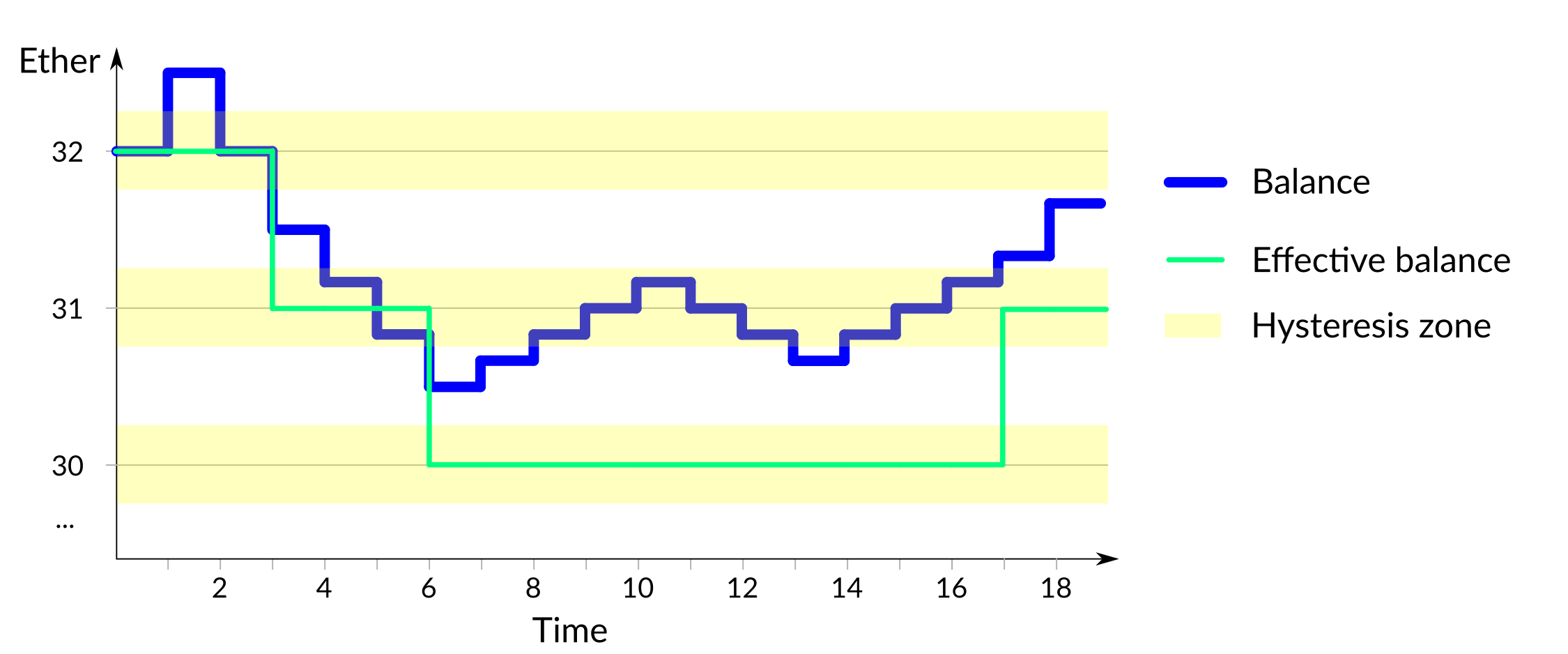Figure 7: Comparison of balance and effective balance

The yellow bands, known as the hysteresis zones, are areas in which effective balance will never change. It can be seen clearly that changes to effective balance only ever occur when the balance moves outside of these zones².

Effective balance was born from a combination of design and technical requirements. On the design side, keeping individual validators to a maximum of 32Ξ stops any single validator from having an excessively large vote in the state of the chain. On the technical side, decreasing the frequency at which effective balance can change means that Ethereum 2 can run on lower-powered hardware, as a change in effective balance necessitates a relatively expensive computation to take place.

With an understanding of effective balance the change in the size of staking rewards and penalties becomes clear. Referring back to the earlier points of confusion:

• at time 3 the validator's balance dropped below 31.75Ξ, resulting in its effective balance going from 32Ξ to 31Ξ as per the fourth rule. Because rewards and penalties are based on effective balance subsequent changes are smaller
• at time 6 the validator's balance dropped below 31Ξ, but was not as low as 30.75Ξ so did not result in a reduced effective balance or size of reward or penalty (although note this does occur at time 7)
• at time 9 the validator's balance rises to 31Ξ, however it does not meet the criteria outlined in the third rule so the effective balance does not increase. Because rewards and penalties are based on effective balance subsequent changes remain as they were
• at time 17 the validator's balance rises above 31.25Ξ, resulting in its effective balance going from 30Ξ to 31Ξ as per the third rule. Because rewards and penalties are based on effective balance subsequent changes are larger, specifically time 18 is the first time at which the increased reward is seen

---

The Impact of Effective Balance on Validating

Because small changes in a validator's balance can have large and long-term effects on its effective balance it is important to keep track of it.

If downtime is required on a validator it is also important to time it correctly, as not all penalties are equal. A 0.015Ξ penalty that drops a validator's balance from 30.010Ξ to 29.995Ξ (with no change in effective balance) has very little impact on the overall rewards generated by the validator, but a 0.015Ξ penalty that drops a validator's balance from 29.760Ξ to 29.745Ξ (with a change in effective balance from 30Ξ to 29Ξ) has a much larger impact.

---

Validator Effectiveness

Validator effectiveness is a metric that shows how much of your validator balance is being used for attesting, calculated as the effective balance as a fraction of the total balance. For example, if a validator has a balance of 31.9Ξ this would result in an effective balance of 31Ξ and its effectiveness would be $\frac{31}{31.9}$, or 97%.

Effectiveness of an active validator will usually be somewhere between 95% and 100%, the higher the better as it maximizes both network security and validator rewards. A low effectiveness suggests a validator has been offline for an extended amount of time. Tracking effectiveness over time is a simple way to measure the overall performance of a validator.

---

A Note on Additional Factors Affecting Rewards

This article shows a simplified view of validating in Ethereum 2 to explain the concept of effective balance. The actual Ethereum 2 rewards and penalties system uses effective balance as a base but rewards vary depending on various factors. Rewards can be higher, for example, if the validator proposes a block. They can also be lower if other validators are offline, or disagree about the state of the chain.

---

Conclusion

Running Ethereum 2 validators successfully requires an understanding of many technical factors, including effective balance. Active management of validators at critical times, for example at times where obtaining a reward or penalty could have a long-term impact on the effectiveness of the validator, can contribute to the overall security of the network and resultant validator rewards. Validator effectiveness over time will prove to be a key metric when understanding the level of active management of funds.

Footnotes

1. In fact the network does not just measure the number of attestations but their cumulative weight: the weight of any given attestation is equal to the effective balance with which the validator attests. ↩

2. The converse is not always true however; at time 13 the balance moves outside of the hysteresis zone but as effective balance is already 30Ξ it remains unchanged. ↩